
by
Brendan McKay
 |
Tolstoy Loves Me by Brendan McKay |
|---|
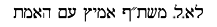
Given two words w,w', a complicated procedure in [WRR] defines a "distance" c(w,w') in the range 0-1 (though sometimes it is "undefined"). To good approximation, random words w,w' will produce a value of c(w,w') uniformly distributed between 0 and 1. Also in [WRR] are several procedures by which a set of numbers in the interval [0,1] are converted into a single number in the same interval. These procedures are called P1 and and P2. P1 and P2 cannot be correctly interpretted as probabilities, but in [WRR] they are used as measures by which several different sets of numbers can be compared. Small values of P1 and P2 indicate "close matching", and large values indicate lack of matching.
) = Alef B = Beit G = Gimmel D = Dalet H = Hey W = Waw Z = Zain X = Chet + = Tet Y = Yud K = Kaf L = Lamed M = Mem N = Nun S = Samech ( = Ain P = Pey C = Tzadi Q = Kuf R = Reish $ = Shin T = TavMy name is Brendan McKay, which in Hebrew is most correctly written BRNDN MQYY. With regard to spellings, there is no question about BRNDN, as the final "a" of Brendan is not pronounced at all, and certainly is not "o" or "oo". The name McKay can conceivably be spelt in other ways, but the use of only one K or Q correctly reflects the pronunciation, which is not Mc'Kay but M'Kay. In any case, the spelling MQYY was the one independently chosen by the Israeli newspaper Maariv, on the single occasion that I have been named in the Israeli press (May 29, 1997).
My place of residence for the past 14 years has been Canberra, Australia. The Hebrew spellings of these names according to the Encyclopedia Hebraica are QNBRH and )WS+RLYH.
My date of birth was October 26, 1951. In the Jewish calendar, that was 26 Tishri 5712.
To perform the experiment, we must convert the data into words, limiting ourselves to the range 5-8 letters as in [WRR].
Firstly, following [WRR], we make a list of appellations. There are only two obvious ones: BRNDN and DR MQYY. Others are too long (BRNDN MQYY, DR BRNDN MQYY) or too short (MQYY). (The method of [WRR] requires 5-8 letters.) The use of DR for representing my title is common in Israel; for example it appears on office doors in university departments. I do not hold the rank of Professor according to the rules of my University, and so am not entitled to use appellations with that title.
To make the date 26 Tishri 5712 into words, we use precedents from earlier experiments. Firstly, we follow [WRR] in writing 26 Tishri as KWT$RY, BKWT$RY and KWBT$RY. Secondly, we follow [HNGM] in writing 5712 as BT$YB, HT$YB, BHT$YB, $NTT$YB, B$NTT$YB, and $NTHT$YB. (The other two, T$YB and B$NTHT$YB are outside the 5-8 length range.)
w = BRNDN DR MQYY
w'
KWT$RY 0.1120 0.0480
BKWT$RY 0.2542 0.1441
KWBT$RY 0.1557 0.1393
BT$YB 0.3200 0.4160
HT$YB 0.0720 0.0160
BHT$YB 0.0240 0.0720
$NTT$YB 0.1368 0.0211
B$NTT$YB undef undef
$NTHT$YB 0.7500 0.8750
QNBRH 0.0880 0.0081
)WS+RLYH undef undef
Values marked "undef" are undefined according to the rules of [WRR].
The values of P1 and P2 are:
Date only Date and Place
P1 : 0.0000326 0.00000252
P2 : 0.0002415 0.00001971
The first method of obtaining a significance level will be to
try alternates to the two appellations, namely rearrangements
of the letters. For example, instead of BRNDN we try BNNDR,
NDBRN etc.. This approach was used in [M] to analyse the
famous Aaron cluster.
Since the calculation of c(w,w') uses words running both forwards and backwards, and each appellations contains one letter twice, there are 30 distinct permutations of BRNDN and 180 of DRMQYY. In combination, there are 30*180 = 5400 distinct pairs of appellations. We tried every one of these appellation pairs and calculated the P1 and P2 scores. Here are the results:
P1 P2
Best: BRNDN, DRMQYY 0.0000326 0.0002415
Next best: DBRNN, DRMQYY 0.0002476 0.0008575
Best derangement: DBRNN, RDQYMY 0.0070036 0.0030297
The correct spelling wins by a factor of 7.6 for P1, and
by a factor of 3.6 for P2. The third line shows the best
combination of two misspellings. It is worse by a factor
of 215 for P1, and a factor of 12.5 for P2.
P1 P2
Best: BRNDN, DRMQYY 0.0000025 0.0000197
Next best: BRNDN, RYQDMY 0.0000224 0.0000767
Best derangement: BDRNN, RYQDMY 0.0009109 0.0006115
The correct spelling wins by a factor of 9.0 for P1, and
by a factor of 3.9 for P2. The third line shows the best
combination of two misspellings. It is worse by a factor
of 364 for P1, and a factor of 31 for P2.
Using the date only Using both date and place
P1 P2 P1 P2
4 9 2 2
Here again we see consistent significance levels below 1 in
1000, completely confirming our expectations.
Did it happen by chance? Yes!
The image at the top of the page shows "Canberra" and
"Dr McKay".
Back to the Mathematical Miracles page
Copyright Brendan McKay (1997),
bdm@cs.anu.edu.au.
Overview on numerical features in different scriptures
Answering Islam Home Page